Počítačové zadanie: Štvorce - pre expertov
Skryť detaily | Obľúbený- Kvalita:73,1 %
- Typ:Počítačové zadanie
- Univerzita:Trenčianska univerzita Alexandra Dubčeka v Trenčíne
- Fakulta:Fakulta mechatroniky
- Kategória:Technika
- Podkategória:Informatika
- Predmet:Základy informatiky
- Autor:xxmiloss
- Ročník:1. ročník
- Rozsah A4:1 strán
- Zobrazené:1 699 x
- Stiahnuté:5 x
- Veľkosť:0,1 MB
- Formát a prípona:MS Office Word (.doc)
- Jazyk:slovenský
- ID projektu:2035
- Posledna úprava:06.09.2016
Majme celé číslo n a ďalej celé čísla x1, x2, ..., x3n. Postupnosť čísel x1, x2, ..., x3n určuje n štvorcov v kartézskej sústave nasledovne: x1, x2 sú súradnice stredu štvorca a x3 je dĺžka strany prvého štvorca; x4, x5 sú súradnice stredu druhého štvorca a x3 je dĺžka strany druhého štvorca. Existujú nejaké body, ktoré patria všetkým štvorcom? Ak také body existujú vypíšte najmenšie takéto súradnice, ak neexistujú vypíšte "nie" (bez úvodzoviek).
Vstup: n, (1<n<100), následne postupnosť x1, x2, ..., x3n.
Výstup: Súradnice najmenšieho spoločného bodu (POZOR, čísla musia byť s 2-mi desatinnými miestami a oddelené jednou medzerou.)
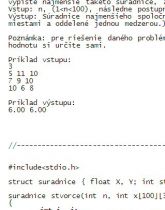
Poznámka: pre riešenie daného problému vytvorte funkciu strvorce(). Parametre a návratovú hodnotu si určite sami.
Príklad vstupu:
3
5 11 10
7 9 10
10 6 8
Príklad výstupu:
6.00 6.00
Vstup: n, (1<n<100), následne postupnosť x1, x2, ..., x3n.
Výstup: Súradnice najmenšieho spoločného bodu (POZOR, čísla musia byť s 2-mi desatinnými miestami a oddelené jednou medzerou.)
Poznámka: pre riešenie daného problému vytvorte funkciu strvorce(). Parametre a návratovú hodnotu si určite sami.
Príklad vstupu:
3
5 11 10
7 9 10
10 6 8
Príklad výstupu:
6.00 6.00