Seminárna práca: Harmonická analýza - matematické metódy, použitie bázových funkcií, frekvenčné spektrum a jeho vplyv na el.zariadenia
Skryť detaily | Obľúbený- Kvalita:93,9 %
- Typ:Seminárna práca
- Univerzita:Trenčianska univerzita Alexandra Dubčeka v Trenčíne
- Fakulta:Fakulta mechatroniky
- Kategória:Technika
- Podkategória:Elektrotechnika
- Predmet:Elektrotechnika 1
- Dokumentácia:Stiahni
- Ročník:2. ročník
- Rozsah A4:11 strán
- Zobrazené:7 260 x
- Stiahnuté:90 x
- Veľkosť:0,2 MB
- Formát a prípona:MS Office Word (.doc)
- Jazyk:slovenský
- ID projektu:6275
- Posledna úprava:15.09.2017
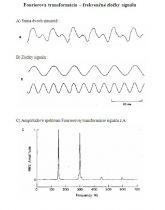
Harmonická analýza sa zaoberá rozkladom signálu na harmonické zložky. Matematický popis harmonického priebehu vyjadruje Fourierov rozvoj.
1.1 Päť základných pravidiel harmonickej analýzy.
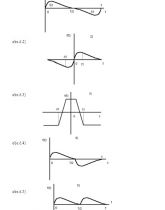
a) Funkcia, ktorej plocha je v intervale ‹0,T) je časovou osou rozdelená na dve rovnaké časti, nemajú teda jednosmernú zložku. Platí tu : a0 = 0 ; (viď obr.1)
b) Funkcia stredovo súmerná podľa začiatku má iba sínusové zložky Fourierovej rady. Pre tieto funkcie platí : -f (t1) = f (-t1) ; (viď obr.2)
c) Funkcia osovo súmerná podľa osi f(t) majú iba kosínusové zložky Fourierovho rozvoja. Platí tu : f (-t1) = -f (t1) ; (viď obr.3)
d) Funkcia, ktorej priebeh sa z prvej polovice periódy opakuje v druhej polovici s opačným znamienkom, majú vo Fourierovom rozvoji len nepárne harmonické zložky. Pre tieto zložky platí : f(t+T/2) = -f(t) ; (viď obr.4)
e) Funkcia, ktorej priebeh sa z prvej polovice periódy opakuje v druhej polovici s rovnakým znamienkom, majú vo Fourierovom rozvoji len párne harmonické zložky. Pre tieto zložky platí : f(t+T/2) = f(t) ; (viď obr.5)
1.1 Päť základných pravidiel harmonickej analýzy.
a) Funkcia, ktorej plocha je v intervale ‹0,T) je časovou osou rozdelená na dve rovnaké časti, nemajú teda jednosmernú zložku. Platí tu : a0 = 0 ; (viď obr.1)
b) Funkcia stredovo súmerná podľa začiatku má iba sínusové zložky Fourierovej rady. Pre tieto funkcie platí : -f (t1) = f (-t1) ; (viď obr.2)
c) Funkcia osovo súmerná podľa osi f(t) majú iba kosínusové zložky Fourierovho rozvoja. Platí tu : f (-t1) = -f (t1) ; (viď obr.3)
d) Funkcia, ktorej priebeh sa z prvej polovice periódy opakuje v druhej polovici s opačným znamienkom, majú vo Fourierovom rozvoji len nepárne harmonické zložky. Pre tieto zložky platí : f(t+T/2) = -f(t) ; (viď obr.4)
e) Funkcia, ktorej priebeh sa z prvej polovice periódy opakuje v druhej polovici s rovnakým znamienkom, majú vo Fourierovom rozvoji len párne harmonické zložky. Pre tieto zložky platí : f(t+T/2) = f(t) ; (viď obr.5)